Mathematics |
|
 |
2007, No. 6
V.A. Kushmantseva
ISOMETRIC SHIFT ON Lp[0, 1], 1 ≤ p < ∞
In the paper it is proved that if isometry T of Lp[0, 1] is determined by a measure nonpreserving transformation of [0,1], then the set of functions for which orbits under isometry T are equivalent to the usual basis of lp, is a dense set in Lp. Analogous problems are discussed. As a mathematical tool a property of almost transitivity of Lp space is used.
O.Y. Danilkina
A NON-LOCAL PROBLEM FOR THE HEAT EQUATION
In the paper a non-local problem with integral condition for the heat equation is considered. The existence and uniqueness of the solution are proved.
D.E. Shafranov
In the paper the Cauchy problem for the linear Oskolkov system is reduced to the the Cauchy problem for the linear Sobolev type equation. The existence of invariant spaces and the dichotomy of solutions the Cauchy problem for the linear Oskolkov system in the k-form spaces defined on the oriented compact Riemannian manifold without boundary are proved.
S.V. Popov, S.V. Potapova
SOLVABILITY OF 2n-PARABOLIC EQUATIONS WITH VARYING EVOLUTION DIRECTION
In the paper the Hölder solvability of 2n-parabolic equations with varying evolution direction is considered. It is shown that Hölder class of solutions essentially depends on Hölder constant and forms of pasting conditions. Necessary and sufficient conditions in the terms of the data of the initial problem are given.
V.A. Alyakin, D.E. Klepnev
DIAGONAL CONTINUOUS SEQUENCES OF MEASURES
A notion of diagonal continuous sequences of measures is introduced. A criterion of uniform absolute continuity for two sequences of measures is obtained. It is possible to consider this criterion as a sequential analogue of well known theorem stating equivalence of absolute continuity and nil-continuity of two measures.
N.S. Baklashova
AN IKUTA THEOREM CONTACT ANALOGUE
In the paper it is proved that integral manifolds of the involutive subdistribution of the Kähler distribution of locally conformal Quasi–Sasakian manifold with a parallel contact Lie form and a C-invariant K?ahler distribution are completely real submanifolds.
Î.À. Vikhreva
In the paper a class of Sobolev’s weight spaces is studied. Moreover, the generalized and Fredholm’s solubility theorems for the mixed boundary value problem for an elliptic equation of the second order generating on base of cylindrical domain are proved.
A.N. Komlev, S.Ya. Shatskih
CONDITIONAL DISTRIBUTION AS A TRANSFORMATION OF INDEPENDENCE OF RANDOM VARIABLES
The paper deals with the conditional distributions of the corresponding systems of random variables as a transformation of independence. In the case of variables with the smooth joint distribution function it is shown, that the conditional distribution is an example of the transformations of independence.While for systems of discrete random variables the conditional distribution does not have a similar property. With the transformations of independence related properties of the joint distributions of random variables which have reproducibility of multivariate conditional quantiles under the restriction to univariate conditional quantiles are studied.
N.V. Nagul
THE PROBLEM OF PRESERVATION OF MANY-SORTED ALGEBRAIC SYSTEM PROPERTIES
In the paper an algorithm for the synthesis of many-sorted system properties preservation criteria is proposed. The conditions obtained are of morphisms character. Examples of application of the algorithm described to studying properties of automata network and general dynamic system are presented.
A.R. Pavlov, M.V. Matveeva
ITERATIVE FINITE-DIFFERENCE SCHEME FOR THE PROBLEM OF HEAT AND MASS TRANSFER IN FREEZING GROUNDS
The numerical solution of the freezing grounds problem is considered. The implicit finite-difference scheme is constructed. The iterative scheme is defined. Convergence of the used finite-difference scheme is proved.
Ò.À. Safonova
DIRIHLET’S PROBLEM FOR A MIXED TYPE EQUATION OF THE SECOND ORDER
In the works of Egorov I.E., Pyatcov S.G., Popov S.V. and others new problems for equation of mixed type are proposed. The Dirichlet’s problem for equation of mixed type is studied in the paper. The common solution of problem is studied by the Fourier method. The unknown function expansion is passed by eigenfunctions of the one nonclassical spectral problem.
E.A. Abapolova, A.P. Soldatov
LAME SYSTEM OF ORTHOTROPIC PLANE ELASTICITY
The representation of general solution of orthotrop Lame system throw vector- value functions analytic in a Douglis sense is given. It is explicitly described by roots of the characteristic equation of Lame system. Using this representation the equivalent reduction of based boundary value problems to singular integral equations is shown.
T.A. Sribnaya
ON THE EXTENSION OF SET FUNCTIONS WITH VALUES IN PARTIALLY ORDERED SEMIGROUPS
In the paper the theorem on the extension of continuous on the right at the
origin, exhaustive quasitriangular submeasures with values in partially ordered
semigroups from m-class Σ to σ-ring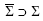 
is proved.
M.S.Tulasynov
In this paper the author investigates the correctness of boundary value problem for a singular parabolic equation with the Bessel operator in a Hölder classes for the case of full matrix of pasting conditions.
O.P. Filatov
APPROXIMATION OF LIMITS OF MAXIMAL MEANS
The problem of the limits of maximal means for the real functions is considered. The supremum for means is evaluated over all solutions of the system of the differential inclusions with the heterogeneous variables. The rate of change of the variables is characterized by small parameters. So the problem of the evaluation of the limits is reduced to some more simple problems. The accuracy of the approximation of the limits of maximal means is found.
O.P. Filatov
THE EULER APPROXIMATIONS AND AVERAGING DIFFERENTIAL INCLUSIONS
The accuracy of the approximation of the solutions of the one-sided Lipschitz differential inclusions with slow and fast variables by means of the Euler integral discrete scheme is found. The averaging theorem for the differential inclusions is derived from the base theorem.
T.U. Sherstyuk
Baskakov’s operators were determined by V.A. Baskakov in 2001. At present
time approximate properties of operators are studied by such mathematicians
U.G. Abakumov, E.S. Kogan, T.V. Dubrovina.
The result including the solution of the evaluation of approximation of function
by trigonometric Baskakov’s operators problem is proved in the paper.
These functions have continuous derivative of the (i ? 1)th order. The derivative
of the first order have discontinuity of the first kind. The theorem is
based on auxiliary propositions, which are given with their proofs.
Some characteristics of Baskakov’s operators are studied.
O.A. Yakubovskaya
It is shown, that the Temlyakov I-kind integral defines an analytic function on a unit hypersphere, if the density function satisfies some special conditions. Outside this hypersphere, the function is represented by the integral, not analytic in the usual sense. In the paper such sufficient conditions for density function, that the function represented by Temlyakov I-kind integral would be analytic in some other domains, not only in unit hypersphere are obtained. Besides, full descriptions of such moving analytical domains are given in the paper.