Математика |
|
2007, № 6
В.А. Кушманцева
ИЗОМЕТРИЧЕСКИЙ СДВИГ В ПРОСТРАНСТВАХ Lp[0, 1], 1 ≤ p < ∞
В работе доказано, что если изометрия T пространства Lp[0, 1] порождена несохраняющим меру автоморфизмом отрезка [0,1], то множество функций, чьи орбиты относительно изометрии T эквивалентны естественному базису пространства lp, образуют плотное множество в пространстве Lp. Рассмотрены близкие к указанному факту задачи. В качестве математического инструмента использована почти транзитивность группы изометрий пространства Lp.
О.Ю. Данилкина
ОБ ОДНОЙ НЕЛОКАЛЬНОЙ ЗАДАЧЕ ДЛЯ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ
В работе рассматривается нелокальная задача с интегральным условием для уравнения теплопроводности. Доказана теорема о существовании единственного обобщенного решения.
Д.Е. Шафранов
В этой работе проведена редукция задачи Коши для линейной системы Осколкова к задаче Коши для линейного уравнения соболевского типа. Доказано существование инвариантных пространств и дихотомии решений задачи Коши для линейной системы Осколкова в пространстве k-форм, определенных на ориентированном компактном римановом многообразии без края.
C.В. Попов, C.В. Потапова
РАЗРЕШИМОСТЬ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ 2n-ГО ПОРЯДКА С МЕНЯЮЩИМСЯ НАПРАВЛЕНИЕМ ЭВОЛЮЦИИ
В работе рассматриваются параболические уравнения 2n-го порядка с меняющимся направлением эволюции, связанные с применением теории сингулярных интегральных уравнений. Устанавливается разрешимость краевых задач в пространствах Гельдера. Показано, что гельдеровские классы их решений существенно зависят как от форм условий склеивания при выполнении необходимых и достаточных условий на данные задачи, так и от нецелого показателя.
В.А. Алякин, Д.Э. Клепнев
ДИАГОНАЛЬНО НЕПРЕРЫВНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МЕР
Введено понятие диагональной непрерывности последовательности мер и получен критерий равностепенной абсолютной непрерывности двух последовательностей мер. Этот критерий можно рассматривать как секвенциальный аналог известной теоремы об эквивалентности абсолютной непрерывности и нуль-непрерывности для двух мер.
Н.С. Баклашова
КОНТАКТНЫЙ АНАЛОГ ТЕОРЕМЫ ИКУТЫ
Доказано, что интегральные многообразия инволютивного подраспределе- ния келерова распределения локально конформно квази-сасакиева многообразия с параллельной контактной формой Ли и C-инвариантным келеровым распределением являются вполне вещественными подмногообразиями.
О.А. Вихрева
В данной работе изучается один класс весовых пространств типа Соболева. Кроме того, доказаны теоремы обобщенной и фредгольмовой разрешимости для смешанной краевой задачи для эллиптического уравнения второго порядка, вырождающегося на основании цилиндрической области.
С.Я. Шатских, А.Н. Комлев
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, КАК ПРЕОБРАЗОВАНИЯ НЕЗАВИСИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН
Рассматриваются системы случайных величин, для которых условные распределения вероятностей являются преобразованиями независимости этой системы. Показано, что для случайных величин имеющих совместную плотность, условные распределения являются примерами возможных вариантов преобразований независимости. Однако для систем дискретных случайных величин условные распределения преобразованиями независимости уже не являются. В связи с изучением свойств преобразований независимости рассматриваются многомерные распределения вероятностей обладающие воспроизводимостью условных квантилей.
Н.В. Нагул
К ВОПРОСУ СОХРАНЕНИЯ СВОЙСТВ МНОГООСНОВНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ
В работе предлагается алгоритм синтеза условий сохранения свойств многоосновных алгебраических систем. Критерии, порождаемые алгоритмом, в частности, требуют, чтобы связывающие системы отображения носили характер морфизмов. Даются примеры использования алгоритма в анализе свойств автоматных сетей и общей динамической системы В.В. Немыцкого.
А.Р. Павлов, М.В. Матвеева
ИТЕРАЦИОННАЯ РАЗНОСТНАЯ СХЕМА ДЛЯ ЗАДАЧИ ТЕПЛОМАССОПЕРЕНОСА ПРИ ПРОМЕРЗАНИИ ГРУНТОВ
В работе рассмотрено численное решение задачи о промерзании грунта. Построена неявная разностная схема, для численной реализации которой определена итерационная схема, доказана ее сходимость.
Т.А. Сафонова
ЗАДАЧА ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ СМЕШАННОГО ТИПА ВТОРОГО ПОРЯДКА
В работах С.Г. Пяткова, И.Е. Егорова, С.В. Пяткова и других поставлены и исследованы новые задачи для уравнений смешанного типа. В этой статье рассматривается задача Дирихле для уравнения смешанного типа. При этом используется метод Фурье, причем разложение неизвестной функции проводится по собственным функциям одной неклассической спектральной задачи.
Е.А. Абаполова, А.П. Солдатов
СИСТЕМА ЛАМЕ ТЕОРИИ УПРУГОСТИ В ПЛОСКОЙ ОРТОТРОПНОЙ СРЕДЕ
Дано представление общего решения системы Ламе в ортотпропном случае через вектор-функции, аналитические по Дуглису. Оно описано явно в терминах корней характеристического уравнения системы Ламе. Пользуясь этим представлением, указана эквивалентная редукция первой и второй краевых задач к системе сингулярных интегральных уравнений на границе области.
Т.А. Срибная
ПРОДОЛЖЕНИЕ ФУНКЦИИ МНОЖЕСТВА СО ЗНАЧЕНИЯМИ В ЧАСТИЧНО УПОРЯДОЧЕННОЙ ПОЛУГРУППЕ
Доказана теорема о продолжении непрерывной сверху в нуле,
исчерпывающей квазитреугольной субмеры со значениями в частично упорядоченной
полугруппе с m-класса Σ на σ-кольцо 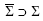 до квазитреугольной субмеры,
непрерывной в нуле на Σ.
до квазитреугольной субмеры,
непрерывной в нуле на Σ.
М.С. Туласынов
В данной работе устанавливается корректность в классах Гельдера краевой задачи для одного сингулярного параболического уравнения с оператором Бесселя в случае полной матрицы склеивания.
О.П. Филатов
АППРОКСИМАЦИЯ ПРЕДЕЛОВ МАКСИМАЛЬНЫХ СРЕДНИХ
Рассматривается задача вычисления пределов максимальных средних для вещественнозначной функции. Точная верхняя граница значений функции вычисляется по всем решениям системы дифференциальных включений с разнотемповыми переменными. Скорость изменения переменных характеризуется малыми параметрами. Это позволяет свести задачу к более простым. Получена оценка погрешности аппроксимации пределов максимальных средних.
О.П. Филатов
АППРОКСИМАЦИИ ЭЙЛЕРА И УСРЕДНЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ВКЛЮЧЕНИЙ
Для односторонне липшицевых дифференциальных включений с быст- рыми и медленными переменными получена оценка погрешности аппроксимации решений с помощью разностной схемы Эйлера. Из этого результата следует теорема усреднения для дифференциальных включений.
Т.Ю. Шерстюк
Операторы Баскакова определены в 2001 году В.А. Баскаковым. В насто-
ящее время аппроксимативные свойства операторов изучаются такими
математиками, как Ю.Г. Абакумов, Е.С. Коган, Т.В. Дубровина и др.
В предлагаемой статье доказан результат, содержащий решение задачи об
оценке приближения тригонометрическими операторами Баскакова функций,
имеющих непрерывную (i ? 1)-ю—производную, при этом i-ая производная
имеет разрыв первого рода. Приведены с доказательством вспомогательные
утверждения, на которых основана теорема. Кроме того, рассмотрены
некоторые характеристики операторов Баскакова.
О.А. Якубовская
В работе В.И. Боганова показано, что интеграл типа Темлякова I рода при определенных условиях, наложенных на функцию плотности, определяет в единичном гипершаре аналитическую функцию. Вне этого гипершара функция, представимая таким интегралом, вообще говоря, аналитической не является. В настоящей работе даны достаточные условия, которым должна удовлетворять функция плотности, чтобы функция, представимая интегралом типа Темлякова I рода, была аналитической и в некоторых других областях, помимо рассматриваемого гипершара. Кроме того, даны полные описания возникающих таким образом подвижных областей аналитичности.