Mechanics |
|
 |
2002, No. 4
A.V. Manzhirov, Y.N. Radayev
TO THE N.KH. ARUTYUNYAN 90th ANNIVERSARY
The paper is dedicated to the Prof. Arutyunyan 90th anniversary. N.Kh. Arutyunyan was born in Yerevan on November 23, 1912.
His academic and research activity started in 1937 at Leningrad Polytechnical Institute under the B.G. Galerkin supervision. In 1949 he was awarded the Doctor of Science (Tech. Sci.) degree from USSR Academy of Sciences. He was the head of the Laboratory of Creep at the Institute of Mathematics and Mechanics of Armenian Academy of Sciences (1955-1961), professor of Dept. of Theoretical Mechanics of Yerevan State University (1951-1958), head of Dept. of Elasticity and Plasticity of Yerevan State University (1958-1975), the rector of Yerevan State University (1961-1975), head of the Laboratory of Viscoelastic Materials at the Institute for Problems in Mechanics of the USSR Academy of Sciences (1975-1993). In 1950 he was elected as member of the Armenian Academy of Sciences, and later in 1959 - as Vice-President of the Armenian Academy of Sciences.
In Armenia Prof. N.Kh. Arutyunyan was also known due to his social and political activity as a member of Armenian SSR and USSR Parliament. In 1962 he was appointed Vice-President of Armenian SSR and occupied this position until 1975.
Prof. N.Kh. Arutyunyan contributed a lot to a several branches of continuum mechanics and mechanics of solids. He is famous for his pioneering works in elasticity, creep, mechanics of ageing, contact mechanics and mathematical modelling of growing solids. He published nearly two hundred original papers and eight books devoted to these fields of continuum mechanics.
Prof. N.Kh. Arutyunyan died in Moscow, January, 18, 1993.
V.M. Pestrikov, V.I. Astafev
TO THE 75-TH ANNIVERSARY OF EUGENY MOROZOV
The paper is dedicated to the 75-th anniversary of Evgeny Michailovich Morozov known as a specialist in fracture mechanics. E.M. Morozov was born in Moscow on December 10, 1927.
His academic and research activity started in 1951 at Moscow Engineering Physics Institute (MEPHI) under prof. Ya.B. Fridman supervision. In 1954 he was awarded the Candidate of Science and in 1971 - the Doctor of Science degree.
E.M.Morozov is the author of well-known books and papers on fracture mechanics - "Elastic-plastic fracture mechanics" (1978), "Mechanics of elastic-plastic fracture" (1989), "Thermal stresses and strength of turbins: calculus and design" (1991), etc.
O.A. Loginov
A FINITE ELEMENT MODELLING BEHAVIOUR OF CONIC SEALING IN A THREADED CONNECTION
A finite element model for the behaviour of conic sealing in a threaded connection is proposed. It is shown that presented model can be used for the determination of optimal parameters of conic sealing.
L.V. Stepanova, Y.N. Ustina
In the present paper, asymptotic fields of stress, strain rate and integrity (continuity)
parameter near the tip of Mode III and Mode I cracks in steady-state growth
are analyzed on the basis of Continuum Damage Mechanics for elastic nonlinearviscous
materials, which deform according to the damage coupled elastic nonlinearviscous
constitutive equation 
, where 
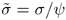, ψ is the continuity
parameter. The nonlinear-viscous term describes power-law creep. The conventional
Kachanov-Rabotnov creep damage theory is utilized and the scalar continuity
parameter is incorporated into the elastic nonlinear-viscous constitutive equation.
The asymptotic stress, strain rate and integrity fields are analyzed by solving a twopoint
boundary value problem of nonlinear differential equations. Three kinds of
the two-point boundary value problems of different nonlinear differential equations
are studied. These three types of the boundary value problems correspond to the
following cases. 1. The asymptotic stress, strain and damage fields are dominated
solely by nonlinear creep terms in the constitutive equation. 2. The linear term of
the constitutive relation governs the asymptotic behaviour as r → 0. 3. The linear
elastic and nonlinear creep terms of the constitutive equations combine to determine
the asymptotic behaviour near the crack tip. The analytical and numerical analysis
given clearly indicate that the second case is realized. Thus, it is shown that the
elastic strain rate cannot be neglected for a growing crack in elastic nonlinear-viscous
damaged materials and the asymptotic stress and damage fields are determined by
the elastic strain rates which have singularity of the type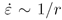 
, where r is the
distance from the current crack tip. It is found that the stress has no singularity
in the vicinity of the growing crack. The non-singular stress field is obtained, as
the damage has such a substantial influence on the material behaviour that the
high stress are relaxed at the crack tip. An analytical expression is obtained which
explicitly shows the variation of stresses while approaching the crack tip. Thus,
the asymptotic solution for stress and strain rate shows quite a different behaviour
compared with those of HRR- and HR-problems. The shapes of the damage process
zone and the totally damaged zone are also determined. These shapes for the Mode
I crack under plane stress and plane strain condition and the Mode III crack
are presented. The contours of the damage fields are represented by the curves
determined analytically for the Mode III crack tip and numerically for the Mode I
crack tip in front of the crack 
and a wake parallel to the crack
plane behind the crack. The law of crack growth is formulated as well.